Fuzzy Sets
Fuzzy Set Hierarchy
Where_are_FuzzySets_Used
Some of the Operations on FuzzySets
A Comment on the Range of Membership Values
A fuzzy set is a mapping of a set of real numbers (xi) onto membership values (ui) that (generally) lie in the range [0, 1]. In this fuzzy package a fuzzy set is represented by a set of pairs ui/xi, where ui is the membership value for the real number xi. We can represent the set of values as { u1/x1 u2/x2 ... un/xn }. The x values in the set are in increasing order (x1 <= x2 <= ... <= xn). Values prior to x1 have the same membership value as x1 and values after xn have the same membership value as xn. Values between xi and xi+1 are determined by the value that lies on the straight line between the 2 consecutive points. In effect we are representing a graph with straight lines joining the points in the fuzzy set and with horizontal lines extending to the first and from the last points.
Just as a side note, it is common for the (x,y) pairs of a fuzzy set to be represented as y/x in the fuzzy logic world. This can be a bit confusing at first because the x,y order is reversed, but it might help to think of the u/x meaning the membership value u at x.
As an example, consider the (convex) fuzzy set { 0.0/0.3 1.0/0.5 0.0/0.7 }. As shown in the diagram below, this is a triangular shaped fuzzy set. This is a very compact representation of a fuzzy set that covers all values in the real number line.
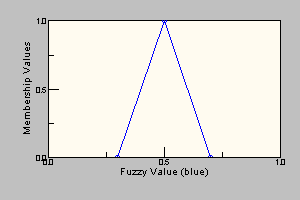
The code to create this FuzzySet would simply be:
FuzzySet fSet = new triangleFuzzySet( 0.3, 0.5, 0.7 );
Consider now a slightly more complex (non-convex) FuzzySet: { 0.0/0.1 1.0/0.3 0.65/0.4 1.0/0.5 0.0/0.8 }
.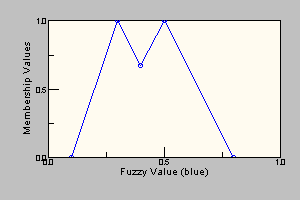
The code to create this 5 point fuzzy set might look something like:
double yValues[] = {0, 1, 0.65, 1, 0};
double xValues[] = {0.1, 0.3, 0.4, 0.5, 0.8};
FuzzySet fSet = new FuzzySet( xValues, yValues, 5 );
A fuzzy set defined by a single point, for example { 0.5/25 }, represents a single horizontal line (a fuzzy set with membership values of 0.5 for all x values). Note that this is not a single point!
To represent such singletons one might use { 0.0/0.5 1.0/0.5 0.0/0.5 }. This is in effect a graph that has membership values of zero for all x values except at the x value 0.5 where it is 1. This sort of fuzzy set is sometimes used to fuzzify crisp values (when there is no error in the x value). Often a crisp value, such as a temperature reading, is valid only within some tolerance so other fuzzy set shapes are used to fuzzify the value, such as a PIFuzzySet or a TriangleFuzzySet. As of version 1.3 of FuzzyJ, there is a SingletonFuzzySet class that allows for easy creation of singleton FuzzySets:
FuzzySet fSet = new SingletonFuzzySet( 0.5 );
Note that, when possible, the points stored will be optimized in various ways to reduce the number required. For example, if three points in a row have the same y (membership) value then the middle point will be dropped or if the first two or last two points have the same y value then the first or last point will be dropped.
Fuzzy Set Hierarchy
To simplify the creation of FuzzySets a hierarchy of subclasses has been defined. The FuzzySets that can be built by this set of subclasses represents a fairly complete set of common shapes. The user is able to sub-class and generate further types to meet specific needs. The hierarchy is shown below.
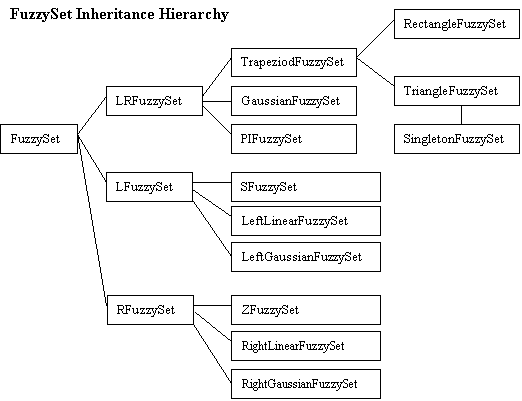
Each of these is explained in more detail in the API documentation. However, let's consider the TriangleFuzzySet briefly. It is a sub-class of (specialization of) a TrapezoidFuzzySet since it is basically a trapezoid shape where the left and right sides of the trapezoid meet at the same point. The TrapezoidFuzzySet is a sub-class of the LRFuzzySet which defines shapes that have a left (L) part, a right (R) part and a middle part (with all values set to 1). The left part slopes from a y-value (membership value) of 0 to 1 and can have various shapes. The right part slopes from a y-value of 1 to 0, and again can have various shapes. The TrapezoidFuzzySet is just an LRFuzzySet with both the left and right parts being linear. The LRFuzzySet and the TrapezoidFuzzySet are shown below.
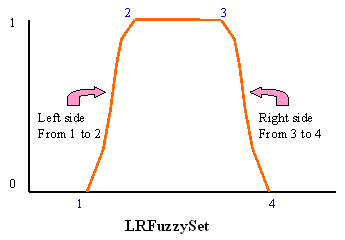
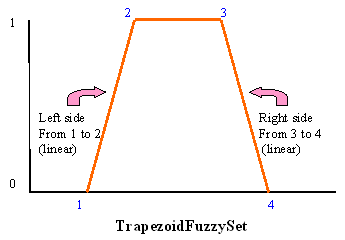
To repeat, the TrapezoidFuzzyset is an LRFuzzySet with the left and right sides
defined to be linear rather than arbitrary shapes. The TriangleFuzzySet is a
TrapezoidFuzzySet with points 2 and 3 at the same location. In terms of
simplicity of generation the TrapezoidFuzzySet can be defined with 4
x-coordinates and the TriangleFuzzySet only needs 3 x-coordinates, whereas the
LRFuzzyset requires that the 4 x-coordinates plus two functions that determine
the shape of the left and right sides. The simple RectangleFuzzySet only needs
2 x-coordinates to be defined.
Where are Fuzzy Sets Used
Although one can create Fuzzy Sets and perform various operations on them, in general they are mainly used when creating Fuzzy Values and to define the linguistic terms of Fuzzy Variables. This is described in the section on Fuzzy Variables. At some point it may be an interesting exercise to add FuzzyNumbers to the toolkit. These would be specializations of FuzzySets with a set of operations such as addition, subtraction, multiplication and division defined on them.
Some of the Operations on FuzzySets
The API documentation describes a large number of operations and manipulations that can be applied to FuzzySets. Most often there is a corresponding capability for FuzzyValues with the restriction that the UOD (universe of discourse, or range of x values) must be observed for the FuzzyValues and for binary operations, such as intersection and union, the two FuzzyValues must have the same FuzzyVariable. The most commonly used operations will be (see the API documentation for the complete set of operations):
fuzzyComplement
Takes the compliment of the FuzzySet. More specifically, it takes the
compliment of the membership (y) values of the SetPoints of the FuzzySet.
Mathematically (NOT), ucompl(x) = 1 - u(x), or ycompl = 1
- y.
fuzzy Intersection
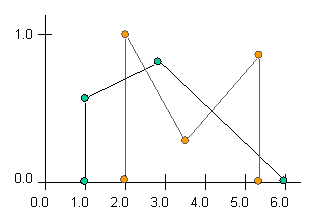
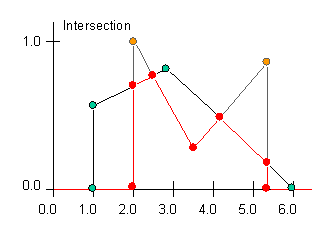
Returns the intersection of two FuzzySets. The visual representation of the
intersection of two example FuzzySets is depicted below. One set is black with
green SetPoints, and the other set is grey with orange SetPoints. The diagram
on the left is of the two FuzzySets, and the diagram on the right is of the two
sets showing the intersection set in red (plain red SetPoints and red lines
joining them). Intersection is synonymous with the logical operator AND. The
intersection of two fuzzy sets is (often and specifically in FuzzyJ) defined
such that the membership (y) value at any x value is the minimum of the
membership values of the two fuzzy sets.
fuzzyUnion
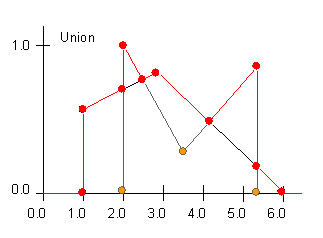
Returns the union of two FuzzySets. The visual representation of the union of
two example FuzzySets is depicted below. One set is black with green SetPoints,
and the other set is grey with orange SetPoints. The diagram on the left is of
the two FuzzySets, and the diagram on the right is of the two sets showing the
union set in red (plain red SetPoints and red lines joining them). Union is
synonymous with the logical operator OR. The union of two fuzzy sets is (often
and specifically in FuzzyJ) defined such that the membership (y) value at any x
value is the maximum of the membership values of the two fuzzy sets.

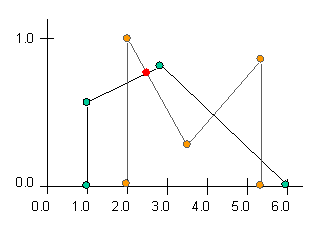
maximumOfIntersection
Returns the maximum membership value of the intersection set formed by two
FuzzySets. Consider the two diagrams below. On the right appears a diagram of
two sets, one set in black with green SetPoints, and the other set in grey with
orange SetPoints. The maximum y value of the intersection is denoted by a red
dot on the graph on the right.

Some Defuzzification Operations on FuzzySets
Below are some methods that convert a FuzzySet back into a single crisp (non-fuzzy) value. This is something that is normally done after a fuzzy decision has been made and the fuzzy result must be used in the real world. For example, if the final fuzzy decision were to adjust the temperature setting on the thermostat a ‘little higher’, then it would be necessary to convert this ‘little higher’ fuzzy value to the ‘best’ crisp value to actually move the thermostat setting by some real amount.
maximumDefuzzify
Finds the mean of the maximum values of a fuzzy set as the defuzzification
value. NOTE: This doesn't always work well because there can be x ranges where
the y value is constant at the max value and other places where the maximum
value is only reached for a single x value. When this happens the single value
gets too much of a say in the defuzzified value.
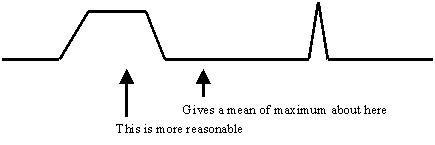
momentDefuzzify
Moment defuzzification defuzzifies a fuzzy set returning a floating point
(double value) that represents the fuzzy set. It calculates the first moment of
area of a fuzzy set about the y axis. The set is subdivided into different
shapes by partitioning vertically at each point in the set, resulting in
rectangles, triangles, and trapezoids. The centre of gravity (moment) and area
of each subdivision is calculated using the appropriate formulas for each
shape. The first moment of area of the whole set is then:
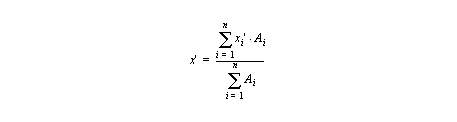
where xi' is the local centre of gravity, Ai is the local
area of the shape underneath line segment (pi-1, pi), and
n is the total number of points. As an example,
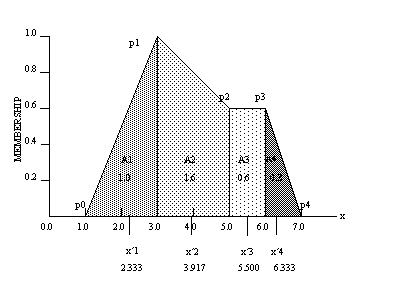
For each shaded subsection in the diagram above, the area and centre of gravity
is calculated according to the shape identified (i.e., triangle, rectangle or
trapezoid). The centre of gravity of the whole set is then determined:
x' = (2.333*1.0 + 3.917*1.6 + 5.5*0.6 + 6.333*0.3)/(1.0+1.6+0.6+0.3) = 3.943…
centerOfAreaDefuzzify (new in version 1.8)
Center of Area (COA) defuzzification finds the x value such that half of the
area under the fuzzy set is on each side of the x value. In the case above (in
the momentDefuzzify section) the total area under the fuzzy set is 3.5
(1.0+1.6+0.6+0.3). So we would want to find the x value where the area to the
left and the right both had values of 1.75. This occurs where x = 3.816699867329622. Note that in general the result
of momentDefuzzify and centerOfAreaDefuzzify are not the same. Also note that
in some cases the center of area can be satisfied by more than one value. For
example, for the fuzzy set defined by the points:
(5,0) (6,1) (7,0) (15,0) (16,1) (17,0)
the COA could be any value from 7.0 to 15.0 since the 2 identical triangles centered at x=6 and x=16 lie on either side of 7.0 and 15.0. We will return a value of 11.0 in this case (in general we try to find the middle of the possible x values).
weightedAverageDefuzzify (new in version 1.3)
Finds the weighted average of the x values of the points that define a fuzzy set using the membership values of the points as the weights. This value is returned as the defuzzification value. For example, if we have the following fuzzy set definition:
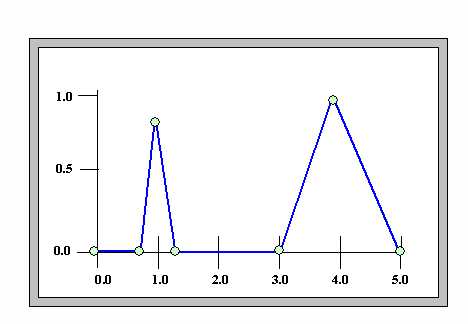
Then the weighted average value of the fuzzy set points will be:
(1.0*0.9 + 4.0*1.0) / (0.9 + 1.0) = 2.579
This is only moderately useful since the value at 1.0 has too much influence on the defuzzified result. The moment defuzzification is probably most useful in this case. However, a place where this defuzzification method is very useful is when the fuzzy set is in fact a series of singleton values. It might be that a set of rules is of the Takagi-Sugeno-Kang type (1st order) with formats like:
If x is A and y is B then c = k
where x and y are fuzzy variables and k is a constant that is represented by a singleton fuzzy set. For example we might have rules that look like:
If temperature is low and pressure is low then set hot valve to medium_high position
If temperature is high and pressure is high then set hot valve to medium_low position
. . .
where the setting of the hot valve has several possibilities, say full_closed, low, medium_low, medium_high, high and full_open, and these are singleton values rather than normal fuzzy sets. In this case medium_low might be 2 on a scale from 0 to 5.
An aggregated conclusion for setting the hot valve position (after all of the rules have contributed to the decision) might look like:
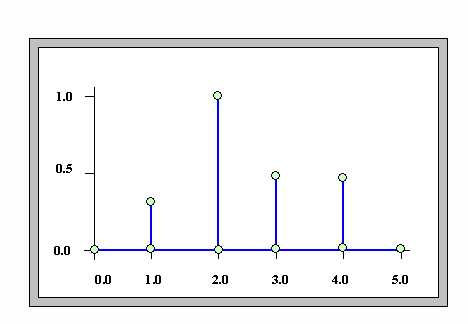
And the weighted average defuzzification value for this output would be:
(1.0*0.25 + 2.0*1.0 + 3.0*0.5 + 4.0*0.5) / (0.25 + 1.0 + 0.5 + 0.5) = 2.556
Note that neither a maximum defuzzification nor a moment defuzzification would produce a useful result in this situation. The maximum version would use only 1 of the points (the maximum one) giving a result of 2.0 (the x value of that point), while the moment version would not find any area to work with and would generate an exception. This description of the weightedAverageDefuzzify method will be clearer after you have completed the sections on FuzzyValues and FuzzyRules.
A Comment on the Range of Membership Values
Although the range of allowed membership values is normally [0, 1], it is possible to form FuzzySets with membership values > 1.0. There are instances where this is desirable. For example in some approaches it is preferred to collect the outputs of fuzzy rules by doing a fuzzySum of the resultant FuzzyValues (global contribution of rules). The fuzzySum operation can result in FuzzySets with membership values > 1.0. When a FuzzySet/FuzzyValue is created with a constructor (that uses arrays of Doubles or an array of SetPoints) the values are restricted to being between 0 and 1. However, when the fuzzySum operation or the methods appendSetPoint and insertSetPoint are used to add points to the FuzzySet, membership values > 1 are allowed.
This does have some implications of which the user needs to be aware. For example, the fuzzyComplement operation on a FuzzySet will treat membership values > 1 as if they were 1. It may be desirable at certain times to normalize (or scale) FuzzySets that have membership values > 1.
Do note that membership values are always restricted to values >= 0. In most cases the negative value is simply changed to a value of 0.
A case where a user might want to allow this to happen is when one wants to use the SAM (Standard Additive Model) method as described in Bart Kosko’s book, Fuzzy Engineering (see reference section). In this case, the collection of fuzzy outputs from multiple rules (global contribution) is done by adding (a fuzzySum of) the outputs. The resultant sum is then defuzzified using the momentDefuzzify method to give the required result. In order to completely perform the SAM method one would also need to ensure that the RuleExecutor was set to be a MamdaniMinMaxMinRuleExecutor and that the operator used to collect the results from multiple antecedents in a rule was the ProductAntecedentCombineOperator. This is explained in more detail elsewhere.