Overview of Fuzzy Concepts
Fuzziness
FuzzyVariable, FuzzySet and
FuzzyValue
FuzzyRule
In the real world there exists much fuzzy knowledge, i.e., knowledge that is vague, imprecise, uncertain, ambiguous, inexact, or probabilistic in nature. Human thinking and reasoning frequently involve fuzzy information, possibly originating from inherently inexact human concepts and matching of similar rather then identical experiences. In systems based upon classical set theory and two-valued logic, it is very difficult to answer some questions because they do not have completely true answers. Humans, however, can give satisfactory answers, which are probably true. Expert systems should not only give such answers but also describe their reality level. This level should be calculated using imprecision and the uncertainty of facts and rules that were applied. Expert systems should also be able to cope with unreliable and incomplete information and with different expert opinions.
Fuzziness
Fuzziness occurs when the boundary of a piece of information is not clear-cut. For example, words such as young, tall, good, or high are fuzzy. There is no single quantitative value which defines the term young when describing a fuzzy concept (or fuzzy variable) such as age. For some people, age 25 is young, and for others, age 35 is young. The concept young has no clean boundary. Age 1 is definitely young and age 100 is definitely not young; however, age 35 has some possibility of being young and usually depends on the context in which it is being considered. In fact an age can have some possibility of being young and also some possibility of being old at the same time (note that these are NOT probabilities and the sum of all the possibilities does not need to sum to 1.0). The representation of this kind of information is based on the concept of fuzzy set theory [Zadeh, Cox, Tsoukalas and Uhrig, Kosko]. Unlike classical set theory where one deals with objects whose membership to a set can be clearly described, in fuzzy set theory, membership of an element in a set can be partial, i.e., an element belongs to a set with a certain grade (possibility) of membership. More formally a fuzzy set A in a universe of discourse U is characterized by a membership function
mA : U ® [0,1]
which associates a number mA(x)
in the interval [0,1] with each element x of U. This number represents the
grade of membership of x in the fuzzy set A (with 0 meaning that x is
definitely not a member of the set and 1 meaning that it definitely is a member
of the set). For example, the fuzzy term young might be defined by the
fuzzy set in the Table below.
|
Fuzzy Term young |
|
|
Age |
Grade of Membership |
|
25 |
1.0 |
|
30 |
0.8 |
|
35 |
0.6 |
|
40 |
0.4 |
|
45 |
0.2 |
|
50 |
0.0 |
One might also write
myoung(25) = 1, myoung(30) = 0.8, ... , myoung(50) = 0
Grade of membership values constitute a possibility distribution of
the term young as applied to the fuzzy variable age. The table
can also be shown graphically (see Figure below).
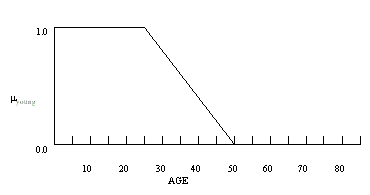
Possibility distribution of young
The possibility distribution of a fuzzy concept like somewhat young or very young can be obtained by applying arithmetic operations to the fuzzy set of the basic fuzzy term young, where the modifiers somewhat and very are associated with specific mathematical functions. For instance, the possibility values of each age in the fuzzy set representing the fuzzy concept somewhat young might be calculated by taking the square root of the corresponding possibility values in the fuzzy set of young (see Figure 1 below). These modifiers are often referred to as hedges. A number of modifiers are supplied with FuzzyJ (see Modifiers).
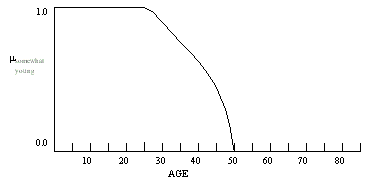
Figure 1: Possibility distribution of somewhat young
FuzzyVariable, FuzzySet and FuzzyValue
Fuzzy concepts are represented using fuzzy variables, fuzzy sets and fuzzy values in the FuzzyJ Toolkit. A FuzzyVariable defines the basic components that are used to describe a fuzzy concept. It consists of a name for the variable (for example, age or hot water temperature) the units of the variable if required (for example, years or Degrees C), the universe of discourse (UOD) for the variable (for example a range from 0 to 125), and a set of fuzzy terms that can be used to describe the particular fuzzy concepts for this variable. The fuzzy terms are described using a term name such as old, along with a FuzzySet that represents that term. The fuzzy variable terms along with a set of fuzzy modifiers (such as very or slightly), the operators and and or (fuzzy set intersection and union respectively) and the left and right parentheses provide the basis for a grammar that allows one to write fuzzy linguistic expressions that describe fuzzy concepts in an english-like manner. These linguistic expressions are encoded in a FuzzyValue which holds a specific fuzzy concept such as age is very old.
For example the linguistic expression,
very old or young
consists of the terms old and young, along with the fuzzy modifier very.
A FuzzyValue is normally created by specifying a FuzzyVariable and a linguistic expression. The example below shows how this is done in Java code.
//definition
of fuzzy variable ‘age’ with terms ‘young’ and ‘old’
FuzzyVariable age
= new FuzzyVariable(“age”, 0, 120, “years”);
age.addTerm(“young”,
new ZFuzzySet(25, 50));
age.addTerm(“old”,
new SFuzzySet(50, 65));
// definition of
FuzzyValue for concept ‘age is somewhat young’
FuzzyValue
ageSomewhatYoung = new FuzzyValue(age, “somewhat young”);
FuzzyJ Code to define the concept 'age is somewhat young'
Without getting into too much detail at this point, above we created a FuzzyVariable, age, that provides the basis for building fuzzy concepts about age. The domain for the variable is from 0 to 120 years and we have defined 2 linguistic terms, young and old, that we can now use to represent specific age concepts. The terms were defined using FuzzySets. In this case young is represented by a sub-class of FuzzySet, ZFuzzySet, which defines a Z-shaped fuzzy set like the one shown in Figure 1 above. Once the FuzzyVariable and the terms that are to be used to describe concepts about that variable are ready, we then can create FuzzyValues. In this case we created an object, ageSomewhatYoung. Note that the definitions of FuzzyValues are actually much more flexible than shown here but this example shows the simplest 'linguistic' (i.e. in english-like phrases) way to create them. Let's also note here that the difference between a FuzzySet and a FuzzyValue may be a bit confusing -- why have both. Ultimately the FuzzyValue is just a FuzzySet (or at least it contains a FuzzySet) but it also has a context, the FuzzyVariable it is associated with. A FuzzySet on its own can be operated on, for example, intersected with another FuzzySet. But this has no real meaning. A FuzzyValue on the other hand can also be manipulated, but only with other FuzzyValues that share the same FuzzyVariable. This is reasonable since doing the intersection of 'hot water' and 'low pressure' makes no sense. This is like adding 5 apples to 6 oranges. Keep this in mind when reading about FuzzySets and FuzzyValues.
FuzzyRule
Now let's continue the example and add a simple FuzzyRule. In general, in rule based systems, rules look something like:
If A1
and
A2
and
...
An
then
C1
and
C2
and
...
Cm
where the Ai are the antecedents on the left hand side (LHS) of the rule and the Cj are the conclusions on the right hand side (RHS) of the rule. In this format, if all of the antecedents (conditions) on the LHS of the rule are true then the rule will fire and the conclusions will be asserted. In the FuzzyJ Toolkit, the fuzzy rules that are supported have FuzzyValue antecedents and FuzzyValue conclusions. (If you are familiar with FuzzyCLIPS then this is equivalent to the so-called fuzzy-fuzzy rules). The rule we are going to build is:
If
temperature is hot and
flow
is low
then
change cold valve positive big amount and
change hot valve zero
We will provide 2 input values to the rule, fire the rule and look at the rule outputs. We'll put this simple example together a bit at a time and show the final results of firing (or executing) the rule. There is a normal sequence of events in the execution of a set of fuzzy rules. First the inputs, which are normally crisp values, are fuzzified. This corresponds to representing the uncertainty in the measure of the inputs (in science class this can be equivalent to reading the value of an instrument like a scale and recognizing that the value is actually plus or minus the reading by some factor that represents the accuracy of the instrument or your ability to read the instrument). It is also required for these rules since the FuzzyValue antecedents must be matched against FuzzyValue inputs. Once the rule has its inputs the rule can be fired. It produces a set of FuzzyValue outputs. These outputs can be left as FuzzyValues but in general, and particularly for this example, we go through a process of defuzzification of the outputs to get crisp (or non-fuzzy) values. This allows the system to take some real world action, such as moving the hot and cold water valves by some real-valued amount.
Step 1 (define the FuzzyVariables for temperature, flow, cold valve change and hot valve change)
//
Temperature Fuzzy Variable has terms cold, OK and hot
FuzzyVariable
outTemp = new FuzzyVariable("temperature", 5.0, 65.0, "Degrees
C");
outTemp.addTerm("cold",
new TrapezoidFuzzySet(5.0, 5.05, 10.0, 35.0));
outTemp.addTerm("OK",
new PIFuzzySet(36.0, 3.5));
outTemp.addTerm("hot",
new SFuzzySet(37.0, 60.0));
// Flow Fuzzy
Variable has terms low, OK, and strong
FuzzyVariable
outFlow = new FuzzyVariable("flow", 0, 100.0,
"litres/minute");
outFlow.addTerm("low",
new TrapezoidFuzzySet(0.0, 0.025, 3.0, 11.5));
outFlow.addTerm("OK",
new PIFuzzySet(12.0, 1.8));
outFlow.addTerm("strong",
new SFuzzySet(12.5, 25.0));
//
hotValveChange has terms NB, NM, NS, Z, PS, PM, and PB which correspond to
// negative
big, negative medium, negative small, zero, positive small,
// positive
medium and positive big
FuzzyVariable
hotValveChange = new FuzzyVariable("hotValveChange", -1.0, 1.0,
"");
hotValveChange.addTerm("NB",
new ZFuzzySet(-0.5, -.25));
hotValveChange.addTerm("NM",
new TriangleFuzzySet(-.35, -.3, -.15));
hotValveChange.addTerm("NS",
new TriangleFuzzySet(-.25, -.15, 0.0));
hotValveChange.addTerm("Z",
new TriangleFuzzySet(-.05, 0.0, 0.05));
hotValveChange.addTerm("PS",
new TriangleFuzzySet(0.0, .15, .25));
hotValveChange.addTerm("PM",
new TriangleFuzzySet(.15, .3, .35));
hotValveChange.addTerm("PB",
new SFuzzySet(.25, .5));
//
coldValveChange has terms NB, NM, NS, Z, PS, PM, and PB which correspond to
// negative
big, negative medium, negative small, zero, positive small,
// positive
medium and positive big
FuzzyVariable
coldValveChange = new FuzzyVariable("coldValveChange", -1.0, 1.0,
"");
coldValveChange.addTerm("NB",
new ZFuzzySet(-0.5, -.25));
coldValveChange.addTerm("NM",
new TriangleFuzzySet(-.35, -.3, -.15));
coldValveChange.addTerm("NS",
new TriangleFuzzySet(-.25, -.15, 0.0));
coldValveChange.addTerm("Z",
new TriangleFuzzySet(-.05, 0.0, 0.05));
coldValveChange.addTerm("PS",
new TriangleFuzzySet(0.0, .15, .25));
coldValveChange.addTerm("PM",
new TriangleFuzzySet(.15, .3, .35));
coldValveChange.addTerm("PB",
new SFuzzySet(.25, .5));
Step 2 (define our rules … in this case only 1 rule is defined)
//
the fuzzy rule ...
// if
temperature is hot and flow is low
// then change
the hot valve zero and the cold valve positive big
FuzzyRule hotLow =
new FuzzyRule();
hotLow.addAntecedent(new
FuzzyValue(outTemp,"hot"));
hotLow.addAntecedent(new
FuzzyValue(outFlow,"low"));
hotLow.addConclusion(new
FuzzyValue(hotValveChange,"Z"));
hotLow.addConclusion(new
FuzzyValue(coldValveChange,"PB"));
Step 3 (provide the fuzzified inputs for the rule)
//
temperature reading is 45.0 degrees C and the flow is 8.0 litres/minute
double showerTemp
= 45.0;
double showerFlow
= 8.0;
// create fuzzy
values from the crisp values
inputTemp =
new FuzzyValue(outTemp, new TriangleFuzzySet(showerTemp-0.05, showerTemp,
showerTemp+0.05));
inputFlow =
new FuzzyValue(outFlow, new TriangleFuzzySet(showerFlow-0.05, showerFlow,
showerFlow+0.05));
Step 4 (execute the rule with these inputs)
// remove any inputs associated with the rule, then
add the new inputs to the rule
// Note: the order inputs are added is important since the inputs must
correspond to the antecedents
hotLow.removeAllInputs();
hotLow.addInput(inputTemp);
hotLow.addInput(inputFlow);
// fire the rule; the result of firing is a special vector of FuzzyValues
that represents the output(s)
FuzzyValueVector fvv = hotLow.execute();
Step 5 (defuzzify the outputs to get crisp values)
//
get the output FuzzyValues from the vector
FuzzyValue
hotValveChangeFval = fvv.fuzzyValueAt(0);
FuzzyValue
coldValveChangeFval = fvv.fuzzyValueAt(1);
// calculate
the deffuzified value
double
crispHotValveChange = hotValveChangeFval.momentDefuzzify();
double crispColdValveChange
= coldValveChangeFval.momentDefuzzify();
Step 6 (let's look at the fuzzy sets of the outputs and the corresponding crisp values)
System.out.println(hotValveChangeFval.plotFuzzyValue("+"));
System.out.println(coldValveChangeFval.plotFuzzyValue("+"));
System.out.println("Defuzzified
hot valve change is: " + crispHotValveChange);
System.out.println("Defuzzified
cold valve change is: " + crispColdValveChange);
The results will appear as follows:
Fuzzy
Value: hotValveChange
Linguistic Value:
??? (+)
1.00
0.95
0.90
0.85
0.80
0.75
0.70
0.65
0.60
0.55
0.50
0.45
0.40
0.35
0.30
0.25
+
0.20
+ +
0.15
0.10
0.05
0.00++++++++++++++++++++++++
++++++++++++++++++++++++
|----|----|----|----|----|----|----|----|----|----|
-1.00 -0.60
-0.20 0.20
0.60 1.00
Fuzzy Value: coldValveChange
Linguistic Value:
??? (+)
1.00
0.95
0.90
0.85
0.80
0.75
0.70
0.65
0.60
0.55
0.50
0.45
0.40
0.35
0.30
0.25
+++++++++++++++++
0.20
0.15
+
0.10
0.05
+
0.00++++++++++++++++++++++++++++++++
|----|----|----|----|----|----|----|----|----|----|
-1.00 -0.60
-0.20 0.20
0.60 1.00
Defuzzified hot valve change is: 0.0
Defuzzified cold
valve change is: 0.6531280609133145
Of course this example is simple and there is much more to be mastered before
one can produce useful fuzzy systems with the NRC FuzzyJ Toolkit. Also the
types of rules and complexity of rules can be enhanced by integration with the Jess rule-based system.